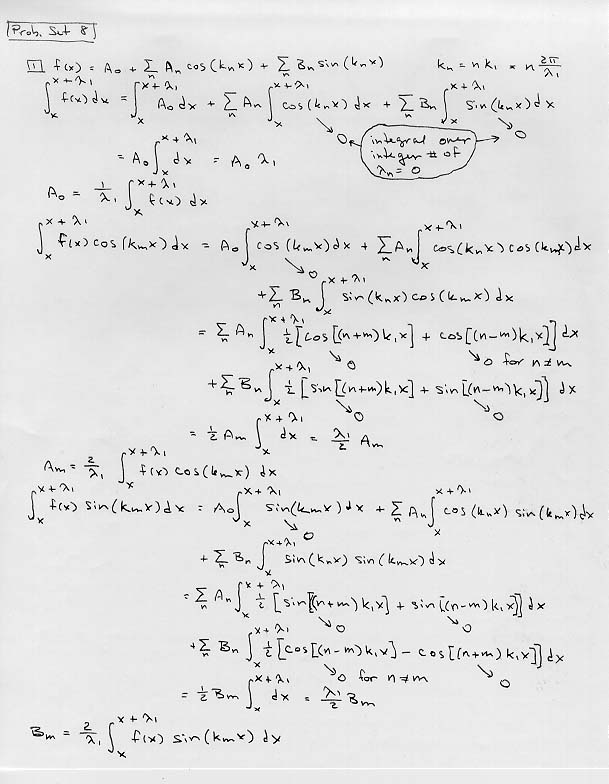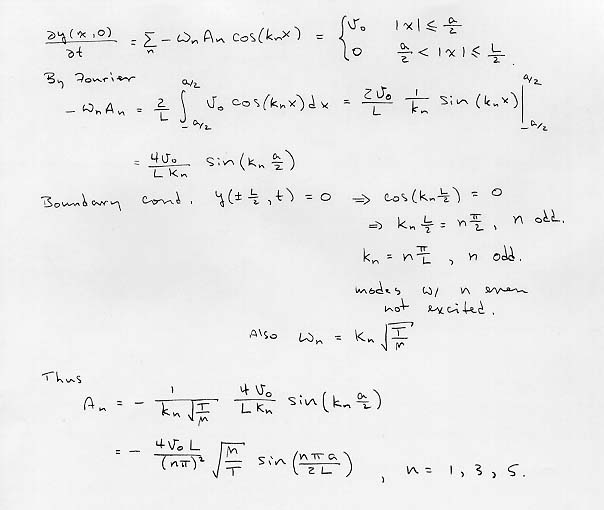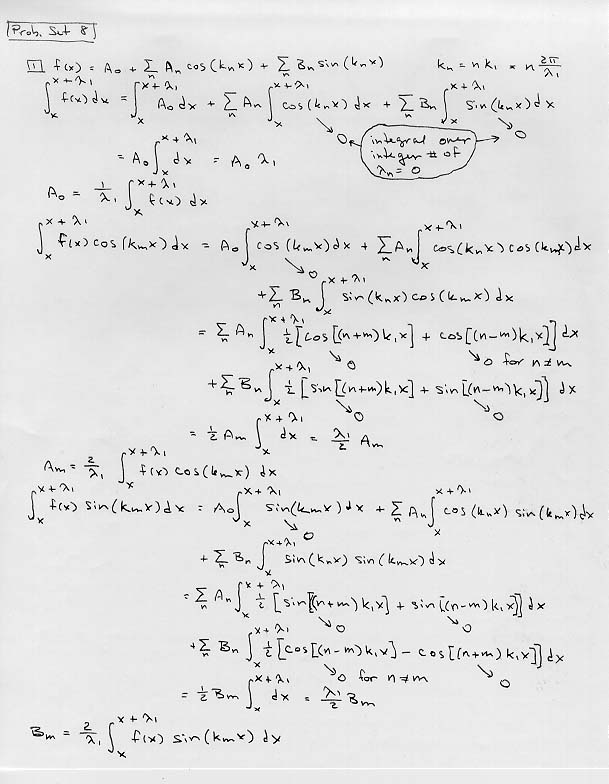
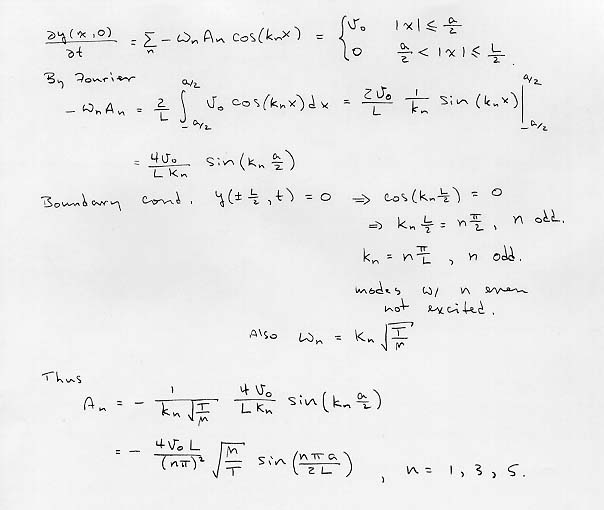
Prob. Set 8 due November 30
 
 
 
 

Problems:
 
 
 
 

1) Derive expressions for the Fourier Series coefficients A_n and B_n as outlined in class. Trigonometric identities you might find useful:

2sin(A)sin(B) = cos(A-B) - cos(A+B)

2cos(A)cos(B) = cos(A+B) + cos(A-B)

2sin(A)cos(B) = sin(A+B) + sin(A-B)
 
 

2) 6-14 (omit part a)
 
 

3) 6-15a
 
 

4) 6-15b
 
 

5) A flexible string of length L is stretched with equilibrium tension T between fixed supports. Its mass per unit length is m. The string is set into vibration with a hammer blow which imparts a transverse velocity v_o to a small segment of length a at the center. Find the amplitudes of the lowest three harmonics excited.